\17\
2. ШТОЛЬНООБРАЗНЫЕ ВЫРАБОТКИ В РЫХЛЫХ ПОРОДАХ
Свои исследования мы начнем следующими общими предпосылками, которые положим в основу расчетов:

1) будем считать, что углы естественных откосов для «несвязных» пород, какими, например, являются песок, галечник и все другие, для которых этот откос не превышает 45°, установлены вполне надежно;

2) давление всего объема породы, приходящегося над выработкой, равно весу этого объема, высота коего доходит до дневной поверхности (вес этого объема, а не давление на крепь);

3) боковое давление, противодействующее вертикальному давлению толщи породы, приходящейся над выработкой, увеличивается по мере удаления от этой выработки в направлении к дневной поверхности (см. стр.14).

Основываясь на этих принципах, мы следующим аналитическим способом определяем искомые силы, действующие на крепь подземных выработок, для расчета величины давления и размеров их крепления.

Пусть мы имеем подземную выработку ABCD (рис.4) на вертикальной глубине h от дневной поверхности.

Рис.4
Представим себе далее, что мы вздумали освободить потолок выработки DC от давления приходящегося над ним призматического объема породы DOMC.

Если для этого начнем извлекать тот вертикальный объем породы, который приходится над выработкой, то едва только мы начнем, например, выбирать часть OILM этого объема, обнаружатся искомые боковые силы, ранее уравновешенные реакцией стенок столба OILM, теперь освобожденные и потому совершающие работу, выражающуюся в перемещении частиц боковой породы по наклонным площадкам KI и TL, представляющим собою естественные откосы. Это перемещение будет продолжаться до тех пор, пока углы KIZ и TLF не станут равны углам естественных откосов для данной породы {ввиду того, что в дальнейших рассуждениях, связанных с выводами кривых обрушения, мы имеем дело с объемами прямых призм (прямоугольных параллелепипедов и прямоугольных призм), боковые ребра которых перпендикулярны плоскости чертежа и равны 1, - для облегчения чтения работы эти тела обозначены фигурами их оснований. Фигуры, являющиеся прямоугольниками, плоскости которых перпендикулярны плоскости чертежа, а одна из сторон лежит в плоскости чертежа, обозначены этими сторонами. Плоскости, перпендикулярные плоскости чертежа, обозначены на чертеже следами их}.

Итак, мы обнаружили существование боковых сил, под влиянием которых сдвигаются по наклонным плоскостям KI и TL призмы КIO и TLM.

Продолжая выбирать дальше столб ODCM, мы обнаружим, что \18\ боковые призмы увеличиваются, а в связи с этим увеличиваются их веса G и G.

Когда будет выбран весь вертикальный объем ODCM, силы G и G будут представлять собою веса призматических объемов HOD и SMC.

Отсюда мы заключаем, что давящую породу над подземной штольнообразной выработкой необходимо рассматривать как состоящую из трех активных объемов: объема ODCM, приходящегося непосредственно над выработкой, и объемов HOD и SCM, сдвигающихся по наклонным плоскостям HD и SC и давящих на вертикальный столб ODCM, создавая трение в плоскостях скольжения OD и МС.

Таким образом, на крепь выработки приходится давление, представляющее собою разность из Q - веса объема породы OMCD - и сопротивления, зависящего от коэффициента трения (тангенса угла естественного откоса), свойственного данной породе, и бокового давления, вызываемого силами G и G.

Как известно из статики сооружений, при давлении грунта на подпорную стенку, в случае отклонения последней, позади нее образуется плоская поверхность скольжения SC (рис.5), по которой происходит обрушение призмы SCM,

Рис.5
Обозначим временно угол, образуемый этой плоскостью скольжения с вертикалью, через . На призму действуют три находящиеся в равновесии силы - сопротивление \19\ пассивной массы земли М, вес призмы G и реакция плоскости МС-Е.

При этом направление силы M образует с нормалью АВ к плоскости скольжения SC угол , равный углу естественного откоса; направление силы Е образует тоже угол трения с нормалью, совпадающей с направлением плоскости МС.

Кроме того, как видно из чертежа, направление G образует с M угол и с Е угол (рис. 5а).

Рис.5a
Когда известна сила G - вес призмы MSC, мы можем построить треугольник сил M, G и Е—LFK (рис. 5а), из которого определяем силу Е по формуле:

откуда:
       (1)
Так как призма MSC ограничена плоскими поверхностями МС и MS, мы по закону Ребхана имеем: MS = SN.

Отсюда

Значит, обрушение пород происходит по плоскости скольжения, наклоненной к вертикали под указанным углом.

Вставив это значение в выражение (1), определяем:
       (1б)
Сделав приведенную предпосылку, перейдем к рассмотрению элемента массы давящей породы высотою dy, находящегося в расстоянии у от вершины свода выработки DNTC (рис. 6).

Рис.6
Если вес единицы объема - , то вес объема ckbd при ширине выработки а:

Выше мы установили, что обрушение породы в случае извлечения призмы ODCM произойдет по плоскости скольжения SC, наклоненной к вертикали под углом

Вес элемента ckbf в этом случае:

Этот элемент находится в равновесии под влиянием уравновешивающих его сил dM, dG и dE, из коих направление dM образует с нормалью \20\ к плоскости SC угол ; тот же угол образует направление dE с нормалью, совпадающей с плоскостью МС вследствие трения в этой плоскости.

Построив силовой треугольник (рис. 6а), мы определяем давление dE на стенку kb:

Рис.6a


Давление на элемент ckbd составит

и сопротивление сдвижению этого элемента

\21\ или после упрощения
        (2)
Сдвижению элемента kbcd сопротивляются 2 dR, или
        (3)
Обозначив
        (4)
имеем:

Остающееся давление элемента ckbd выразится разностью элементарных сил

Обозначив эту разность через dX, имеем:
        (5)
Разделим полученное равенство на dy:

После интегрирования
        (6)
Полученное выражение есть уравнение параболы, и сила X, стало быть, изменяется по закону параболы.

Для определения осей этой параболы необходимо уяснить смысл выражения (5).

Веса элементов вертикального столба OMCD (рис. 6) - dQ - остаются постоянными, независимо от расстояния их от свода выработки в направлении к дневной поверхности, так как объемы их не меняются; элементарные же силы 2dR, зависящие от веса элементов боковых призм, увеличиваются по мере удаления вверх от выработки, так как увеличивается площадь их поперечного сечения по мере приближения к дневной поверхности.

Разность между элементарными силами dQ и 2dR(dx) уменьшается; поэтому, по мере удаления от выработки вверх и на некотором расстоянии от выработки, эта разность dX=0. В этом пункте на основании выражения (5): \22\

Здесь, стало быть

откуда
        (6a)
Выше этого пункта разность между силами dQ и 2dR(dx) не только не оказывает давления на крепь, но для обрушения породы необходимо приложить к элементам ее некоторое усилие.

Таким образом, изменение давления на крепь происходит в пределах от 0 до X, а у — от 0 до .

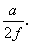Полная сила давления на крепь X получается в результате суммирования разностей между силами, вызываемыми весом элементов в пределах вертикального столба OMCD и в пределах боковых призм MCS и HOD (рис. 6):

Начинаясь от потолка выработки, эти разности dx хотя и уменьшаются по мере удаления вверх от выработки, однако, прибавляясь к разностям элементарных сил dX, вызываемых весом нижележащих элементов, они все же увеличивают давление на крепь X. Это увеличение, как мы видели выше, обнаруживается до того пункта, где разность между элементарными силами dX и 2dR станет равной 0.

Этот пункт, как мы видели, находится в расстоянии

от свода выработки.

На основании выражения (6а) и учитывая изложенное, мы можем записать:

откуда
        (7)
Так как кривая обрушения есть линия параболического типа, естественно считать ее параболой второго порядка, проходящей через концы отрезка CD.

Вес любого параболического объема давящей породы с осями a и b, приходящегося на единицу длины выработки, при объемном весе

В нашем случае

\23\ следовательно,

откуда
        (8)
Таким образом, на свод штольнообразной выработки, пройденной по «несвязным» породам, давит параболический объем породы, ширина которого соответствует ширине этой выработки, а высота зависит от той же ширины последней и величины угла естественного откоса, свойственного данной породе.

Как это вытекает из полученного нами выражения (8), мы разрешаем давнишний спор о том, в какой мере глубина заложения штольнообразной выработки влияет на величину давления породы на ее крепь.

Это выражение устанавливает, что глубина заложения штольнообразных выработок ни в какой мере не влияет на величину давления породы на переклад или на свод их.

Кроме того, из того же выражения вытекает, что величина давления породы на свод штольнообразных выработок не зависит также от высоты их.

В зависимости от этой высоты находится, как мы увидим ниже, лишь величина бокового давления на стену ее или на стойки крепи. Ниже мы также увидим, что влияние глубины заложения штольнообразных выработок проявляется лишь в отдельных частных случаях.

Сравним полученный результат с выражением для высоты параболического объема давящих пород, определенным проф. Протодьяконовым.

По его теории

При этом а - полупролет свода. У нас а - весь пролет.

Если для сравнения придать одинаковое значение для а, то формула проф. Протодьяконова должна принять вид:

Таким образом, полученное нами выражение (8) в
        (8a)
раза больше. \24\

При этом легко видеть, что для любых пород с различными углами естественного откоса от 0 до 45°

По этой причине определяемая по формулам проф. Протодьяконова толщина крепи штольнообразных выработок оказывается в несколько раз тоньше, чем это установлено практикой.

В этом убедился сам проф. Протодьяконов при решении практических примеров, чем только и можно объяснить введение в аналитические формулы двух коэффициентов 2 и 2.

Как видно из выражения (8а), постоянный коэффициент может дать удовлетворительный результат лишь в отдельном частном случае; для пород же с различными углами естественных откосов пришлось бы подбирать и различные коэффициенты.

Совершенно очевидно, что коэффициентами разрешить поставленную задачу нельзя.

Мы, таким образом, теоретически определили форму свода, не руководствуясь практической предпосылкой, что при обрушении пород имеет место образование свода, поверхность которого представляет собою кривую равновесия всех сил.

Сравним также полученную нами формулу (8) с выводом Бирбаумера на конкретных примерах.

Основное отличие нашей теории от теории Бирбаумера, заключается в том, что
1) мы отрицаем влияние глубины заложения штольнообразной выработки на величину давления горных пород на ее крепь и
2) отрицаем также это влияние в зависимости от высоты самой выработки.

Последнее влияние исключается всеми известными нам авторитетными исследователями.

Однако, в частных случаях, когда вертикальное расстояние от дневной поверхности до выработки меньше высоты параболического объема, определенной нашей формулой , давление окажется меньшим вычисленного, так как давить фактически будет меньший объем, чем теоретически определенный, и тем меньший, чем ближе выработка к дневной поверхности, т. е. только лишь до глубины величина давления зависит от вертикального расстояния между дневной поверхностью и выработкой.

Выше мы видели (стр. 10), что лишь в небольших пределах (например, для пород с углом естественного откоса в пределах до глубины 35-40 м) принципиальное наше расхождение с Бирбаумером о влиянии глубины наложения выработок на величину давления па крепь отпадает.

Решим несколько примеров на определение высоты объема давящей породы для штольнообразных выработок, заложенных на различных глубинах в пределах 40 м, по нашему методу и по методу Бирбаумера и сравним результаты решений. \25\

ПРИМЕР

Требуется определить высоту объема давящей породы над штольнеобразной выработкой шириной 3 м, высотой 2 м, пройденной по породам с углом естественного откоса .

По нашему методу

По методу Бирбаумера:
а) для выработки, заложенной на глубине 40 м:




6} для выработки, заложенной на глубине 35 м:


в) для выработки, заложенной на глубине 30 м:


Для больших глубин заложения выводы Бирбаумера не совпадут с нашими, так как на основании математического анализа мы установили, что глубина не оказывает на крепь выработки никакого влияния.

Руководствуясь данными из статики сооружений, а также данными Комерелля, Люкаса и других о давлении пород на крепь подземных штольнообразных выработок, мы составили таблицу углов естественного откоса и объемных весов , свойственных несвязным породам. \26\

1. Таблица значений для и в несвязных породах

№ пп.	Род породы
1	Насыпная неуплотненная  земля	36	1,4
2	Насыпная уплотненная земля	42	1,6
3	Насыпная насыщенная водой земля	28	1,8
4	Песок естественной сырости	33	1,8
5	Песок сухой	30	1,6
6	Плывун	26	1,7
7	Глинистый грунт и глинозем (сухие)	40	1,8
8	Глинистый грунт и глинозем (мокрые)	28	1,9
9	Гравий, галька (сухие)	40	1,85
10	Гравий, галька (мокрые)	30	1,86
11	Плохо окатанная галька	43	2,0
12	Закладка, порода, нарушенная сбросами, сдвигами и др.	45	2,2

Перейдем к выводу формул, определяющих величину давления пород на крепь штольнообразных выработок, пройденных в устойчивых породах.