\26\
7. ВЕРТИКАЛЬНЫЕ ВЫРАБОТКИ В УСТОЙЧИВЫХ ПОРОДАХ
Переходя к другой группе пород, устойчивость которых колеблется от состояния полного разрушения (закладка) с углом трения =45° до абсолютно устойчивых, мы также не можем больше применить приведенные выше выражения.

Лишь для пород, составляющих переход от пород несвязных к связным с углом трения , равным 45°, мы еще применяем формулу (23).

Согласно выражению (23), мы можем определить ось DF полупараболического объема давящей на площадку DC породы (рис. 10).

Так как вес этого объема

и одновременно объем этот с осями DC и DF на всю длину поперечного сечения выработки t весит

то

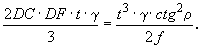
При

       (29)
Для переходной от «несвязных» к устойчивым породам = 45°; в этом случае, подставив значение f из выражения (2la),

       (30)
Если между частицами породы существует сцепление, объем давящей породы, чтобы оторваться и оказать давление на площадку СВ (рис. 11), должен оторваться по поверхности ANB.

Рис.11
Примем временно, с достаточным приближением, что объем давящей породы ANBC имеет форму трехгранной призмы ABC длиною t, равной \48\ длине поперечного сечения вертикальной выработки, и выделим в пределах этого объема бесконечно узкую полоску NO шириною dy, находящуюся на расстоянии у от пункта С.

Заметим предварительно, что

При

и согласно выражению (30)

Определяем:

а при = 45°
       (31)
Вес полоски NO во всю ширину ее t, соответствующей длине поперечного сечения вертикальной выработки


Для того чтобы оторваться, полоске МО нужно преодолеть сцепление, существующее в устойчивой породе, в пункте N.

Если обозначить сцепление на единице поверхности через , то в пункте N это сцепление по всей ширине полоски t


Остающееся давление на площадку СВ в пункте О составит

       (32)
По мере удаления от С к В веса dS уменьшаются, в то время как сцепления dL остаются постоянными. Поэтому давление dx уменьшается, и в некотором расстоянии от С к В разность между dS и dL равна нулю.

Это имеет место, на основании выражения (32), в том пункте между С к В, где

и где

Ближе к пункту В разность становится отрицательной, и элемент NO не только не оказывает давления на площадку СВ, но, чтобы оторвать его, к нему нужно приложить некоторое усилие.

Таким образом, мы установили, что давление на площадку СB \49\ изменяется в пределах от 0 до х, в зависимости от изменения у от 0 до

Исходя из этого и на основании выражения (32) мы можем составить выражение:

откуда:
       (33)
Полупараболический объем ANBC рассматривался нами как призматический ABC, т.е. взят объем меньший действительного в

раза.

Внесем эту поправку в выражение (33):

       (34)
К этому давлению следует прибавить вес обрушающейся по плоскости скольжения наклоненной к вертикали под углом трехгранной призмы , которая одновременно преодолевает сцепление по поверхности BE, ширина коей (при = 45°):


и длина равна длине сечения вертикальной выработки t.

При = 45° площадь этой поверхности

Принимая сцепление на единицу поверхности , сцепление по всей площадке составит

       (35)
Вес призмы СК'Е при = 45°

       (36)
Остающееся давление трехгранной призмы СВЕ составит

       (36a)
\50\ Общее давление полупараболического объема и трехгранной призмы составит

       (37)
Учитывая, что = 45°, и основываясь на прежних выводах (стр. 42), мы можем определить, какому давлению (u) должна быть противопоставлена надежная крепь в части выработки СЕ:


Приняв здесь, как и при проведении штольнообразных выработок в устойчивых породах, объемный вес этих пород = 2,5 т, определяем давление на t м² поверхности вертикальной выработки

;   т/м².
Пренебрегаем слагаемым 0,018 как ничтожной величиной, в особенности при определении давления на 1 см², когда это слагаемое при внесении значения =15 000 кг/м² < кг/см²; имеем окончательно,

  т/м²     (38)
Для расчета толщины крепи обычно требуется определить давление в килограммах на 1 см².

В этом случае наше выражение примет следующий вид:

  кг/см²     (39)
(t - в метрах, - в т/м²).

Этим выражением мы будем пользоваться при расчетах толщины крепления вертикальных выработок в устойчивых породах.

До сих пор мы рассматривали давление на крепь вертикальных выработок прямоугольного сечения. Легко видеть, что наш метод определения давления остается таким же и при расчете давления на крепь вертикальных круглых выработок.

Определенное нами давление Р по формуле (38) распределяется на плоской площадке, ширина и длина коей равна t.

Легко видеть, что в случае круглой шахты EF (рис. 10) представляет собою 2R.

В этом случае одно и то же давление Р распределяется уже не на плоской площадке, а на полукруглой с радиусом R. Давление поэтому на единицу поверхности Р будет меньше в
  раза.
\51\ - площадь половины участка высотою 2R круглой выработки и 2R*2R - площадь такого же участка в прямоугольной выработке, стороны которой для сравнения взяты шириною, равной диаметру круглой шахты – 2R.

Из сказанного вытекает, что давление на 1 см² поверхности круглой выработки меньше такового в прямоугольной, ширина коей равна диаметру этой круглой шахты в
  раза.
С этой точки зрения преимущество вертикальных выработок круглого сечения перед выработками прямоугольного сечения совершенно очевидно.

Таким образом, при определении давления на 1 см² круглой вертикальной выработки следует в формулу (39) подставить 2R вместо t и разделить результат на .

Давление на 1 см² составит
  кг/см²     (40)
Совершенно очевидно, что данный вывод мы можем отнести и к случаю проведения вертикальных выработок в рыхлых породах, подставив в формулу (27) 2R вместо t и разделив его на .

Следовательно, давление в этом случае составит

  кг/см²     (41)
_____________